Метод вычисления спектральной функции полосы с учетом интерференции линий и эффекта доплеровского уширения.
В основу настоящего подхода положена модифицированная модель сильных столкновений [1], позволяющая варьировать интенсивность спектрального обмена между линиями, принадлежащими различным вращательным ветвям полосы. Согласно этой модели, столкновения спектроскопически активной молекулы с частицами окружения можно разбить на два класса: столкновения, происходящие с частотой 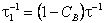 и приводящие к спектральному обмену только между линиями, принадлежащими одной ветви, и столкновения, происходящие с частотой и приводящие к спектральному обмену между всеми линиями полосы, где и приводящие к спектральному обмену только между линиями, принадлежащими одной ветви, и столкновения, происходящие с частотой и приводящие к спектральному обмену между всеми линиями полосы, где  -1 - полная частота столкновений, возмущающая вращательное движение молекулы; CB - параметр модели, характеризующий степень взаимодействия различных вращательных ветвей полосы. Спектральную функцию полосы в рамках такого подхода можно представить в виде: -1 - полная частота столкновений, возмущающая вращательное движение молекулы; CB - параметр модели, характеризующий степень взаимодействия различных вращательных ветвей полосы. Спектральную функцию полосы в рамках такого подхода можно представить в виде:
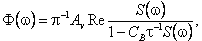 (1) (1)
где
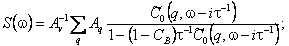 (2) (2)
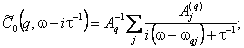 (3) (3)
A(q)j и  qj - интенсивность и частота линии, соответствующей колебательно-вращательному переходу ( qj - интенсивность и частота линии, соответствующей колебательно-вращательному переходу ( i, ji) --> ( i, ji) --> ( i, ji + q); Av - интегральная интенсивность полосы; Aq - интенсивность ветви q. i, ji + q); Av - интегральная интенсивность полосы; Aq - интенсивность ветви q.
Продольный эффект Доплера [2] приводит к неоднородному уширению линий спектра, поскольку наблюдаемые частоты линий  qj для молекул, обладающих величиной V проекции скорости на направление волнового вектора падающего излучения, испытывают смещение qj для молекул, обладающих величиной V проекции скорости на направление волнового вектора падающего излучения, испытывают смещение
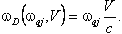 (4) (4)
Вследствие этого, для ансамбля молекул с тепловым распределением значений в отсутствие столкновительных возмущений в спектре будут наблюдаться линии следующей формы
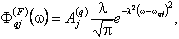 (5) (5)
где
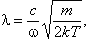 (6) (6)
а m - масса поглощающей молекулы.
Предположим, что столкновения, возмущающие вращательное движение молекулы, приводят также к возмущению ее поступательного движения, и будем считать, что после каждого из столкновений, происходящих с частотой  -1, вероятность значений не зависит от значения V до удара и описывается тепловым распределением. Используя подход, развитый в работе [1], легко показать, что в этом случае выражение (2) для функции S( -1, вероятность значений не зависит от значения V до удара и описывается тепловым распределением. Используя подход, развитый в работе [1], легко показать, что в этом случае выражение (2) для функции S( ), входящей в формулу (1) для спектральной функции, приобретает вид ), входящей в формулу (1) для спектральной функции, приобретает вид
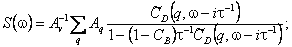 (7) (7)
где
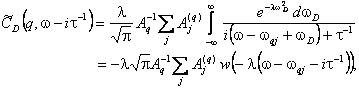 (8) (8)
a 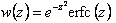 - комплексная функция вероятности [3]. Отметим, что значения этой функции легко могут быть вычислены с использованием простых апроксимационных выражений (см., например, [4]). - комплексная функция вероятности [3]. Отметим, что значения этой функции легко могут быть вычислены с использованием простых апроксимационных выражений (см., например, [4]).
При проведении расчетов спектральной функции с привлечением базы данных HITRAN целесообразно использовать поправочную функцию полосы, определяемую следующим выражением:
 , (9) , (9)
где
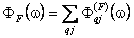 (10) (10)
есть сумма линий, описываемых контуром Фойгта (Voigt) 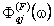 - сверткой доплеровского и лоренцевского контуров. Как и в случае ранее описанной модели [1], алгоритм вычисления спектральной функции полосы с помощью модифицированной модели можно представить в виде трех этапов: - сверткой доплеровского и лоренцевского контуров. Как и в случае ранее описанной модели [1], алгоритм вычисления спектральной функции полосы с помощью модифицированной модели можно представить в виде трех этапов:
- Вычисление функции (10) ФFHITRAN(
 ) на основе параметров линий, содержащихся в базе данных HITRAN, с одновременным определением средней полуширины линий полосы ) на основе параметров линий, содержащихся в базе данных HITRAN, с одновременным определением средней полуширины линий полосы 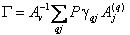 , где , где 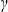 qj - коэффициенты уширения линии, P - давление газа. qj - коэффициенты уширения линии, P - давление газа.
- Вычисление поправочной функции (9) с помощью представленной выше модели при значении
 -1, определенном из средней полуширины линий: -1, определенном из средней полуширины линий: 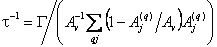 . .
- Вычисление контура полосы с помощью спектральной функции, представленной в виде произведения фойгтовского множителя ФFHITRAN(
 ) и модельной поправочной функции полосы. ) и модельной поправочной функции полосы.
В качестве примера мы произвели расчет небольшого участка в спектре пропускания CO2 в атмосфере Марса на горизонтальной трассе длиной 1 км на высоте около 10 км (давление газа CO2 равно 1 мм рт. ст., температура 200 K), результаты расчета представлены на рисунке.
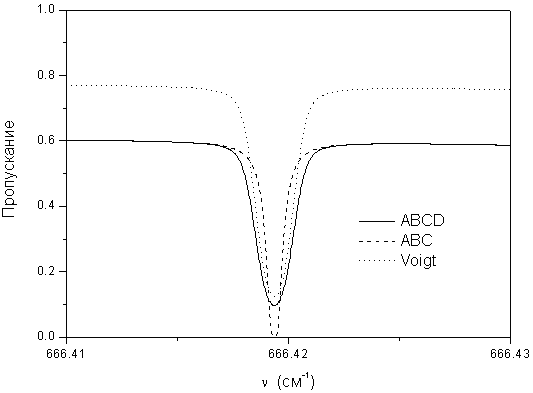
Из рисунка видно, что развитая в настоящей работе модель позволяет одновременно учитывать два эффекта, влияющих на величину пропускания: эффект Доплера и эффект интерференции спектральных линий полосы.
Литература
- M.V. Tonkov, N.N. Filippov, Yu.M. Timofeyev, and A.V. Polyakov. A simple model of line mixing effect for atmospheric application: theoretical background and comparison with experimental profiles. JQSRT, 1996, v.56, pp. 783-795.
- М.А. Ельяшевич. Атомная и молекулярная спектроскопия. Физматгиз, М: 1962, 892 с.
- М. Абрамовиц, И. Стиган. Справочник по специальным функциям. Наука, М: 1979, 830 с.
- J.Humlicek. An efficient method for evaluation of the complex probability function: the Voigt function and its derivatives. JQSRT, 1979, v.21, pp. 309-313.
Филиппов Н.Н. |